Straight Line and Pair of Straight Lines 1 Question 19
19. Let
(2017 Main)
(a)
(b)
(c)
(d)
Show Answer
Solution:
- Given, vertices of triangle are
Thus, the coordinates of vertices of triangle are
Now, equation of altitude from vertex
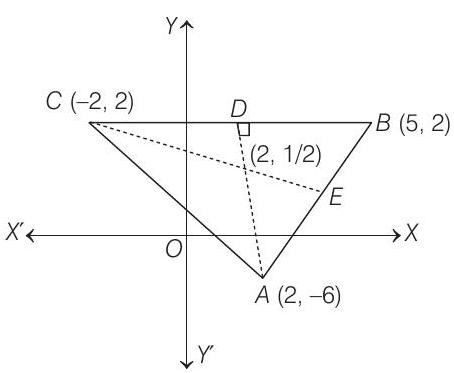
Equation of altitude from vertex
On solving Eqs. (i) and (ii), we get






