Straight Line and Pair of Straight Lines 1 Question 16
16. If the line
(2019 Main, 10 Jan I)
(a)
(b)
(c)
(d)
Show Answer
Solution:
- Given equation of line is
For intersection with
For intersection with
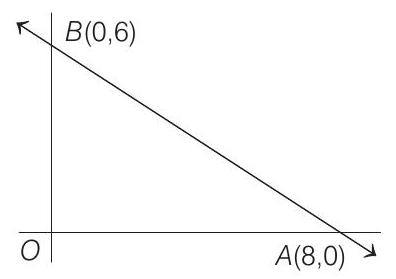
Let
and
Also, let incentre is
and






