Straight Line and Pair of Straight Lines 1 Question 1
1. A straight line
(2019 Main, 12 April II)
(a)
(b)
(c)
(d)
Show Answer
Solution:
- According to the question, we have the following figure.
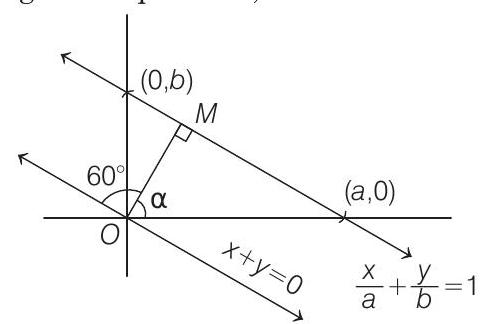
Let
Since, line
So, equation of the line ’






