SATHEE: Properties of Triangles 3 Question 5

Properties of Triangles 3 Question 5

5. In a $△ A B C$ , let $∠ C = π / 2$ . If $r$ is the inradius and $R$ is the circumradius of the triangle, then $2 (r + R)$ is equal to

$(2000, 2 M)$

(a) $a + b$

(b) $b + c$

(d) $a + b + c$

Passage Based Problems

Consider the circle $x^{2} + y^{2} = 9$ and the parabola $y^{2} = 8 x$ . They intersect at $P$ and $Q$ in the first and the fourth quadrants, respectively. Tangents to the circle at $P$ and $Q$ intersect the $X$ -axis at $R$ and tangents to the parabola at $P$ and $Q$ intersect the $X$ -axis at $S$ .

$(2007, 8 M)$

Show Answer

Answer:

Correct Answer: 5. (a)

Solution:

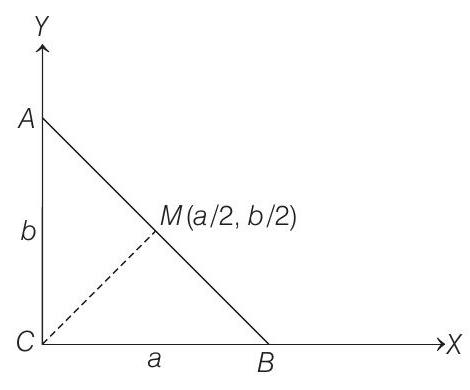
Here, $R^{2} = M C^{2} = \frac{1}{4} (a^{2} + b^{2})$ [by distance from origin] $= \frac{1}{4} c^{2}$ [by Pythagoras theorem]

$\Rightarrow R = \frac{c}{2}$

Next, $r = (s - c) \tan (C / 2) = (s - c) \tan π / 4 = s - c$

$∴ 2 (r + R) = 2 r + 2 R = 2 s - 2 c + c$

$\begin{aligned} = a + b + c - c \\ = a + b \end{aligned}$

पिछला

अगला

Properties of Triangles 3 Question 5

5. In a $△ A B C$ , let $∠ C = π / 2$ . If $r$ is the inradius and $R$ is the circumradius of the triangle, then $2 (r + R)$ is equal to

Passage Based Problems

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Properties of Triangles 3 Question 5

5. In a △ABC, let ∠C=π/2. If r is the inradius and R is the circumradius of the triangle, then 2(r+R) is equal to

Passage Based Problems

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

5. In a $△ A B C$ , let $∠ C = π / 2$ . If $r$ is the inradius and $R$ is the circumradius of the triangle, then $2 (r + R)$ is equal to