Properties of Triangles 3 Question 2
2. Let the equations of two sides of a triangle be $3 x-2 y+6=0$ and $4 x+5 y-20=0$. If the orthocentre of this triangle is at $(1,1)$ then the equation of its third side is
(2019 Main, 9 Jan II)
(a) $122 y-26 x-1675=0$
(b) $26 x-122 y-1675=0$
(c) $122 y+26 x+1675=0$
(d) $26 x+61 y+1675=0$
Show Answer
Answer:
Correct Answer: 2. (b)
Solution:
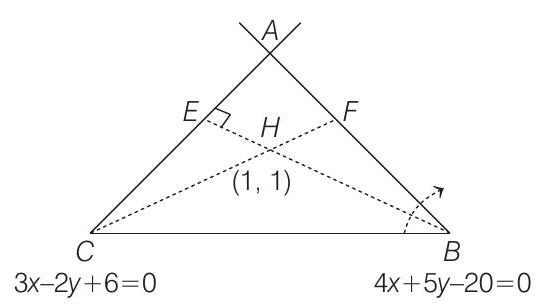
Let equation of $A B$ be $4 x+5 y-20=0$ and $A C$ be $3 x-2 y+6=0$
Clearly, slope of $A C=\frac{3}{2}$
$$ \left[\because \text { slope of } a x+b y+c=0 \text { is }-\frac{a}{b}\right] $$
$\therefore$ Slope of altitude $B H$, which is perpendicular to
$$ A C=-\frac{2}{3} \quad \cdot \because m _{B H}=-\frac{1}{m _{A C}} $$
Equation of $B H$ is given by $y-y _1=m\left(x-x _1\right)$
Here, $\quad m=-\frac{2}{3}, x _1=1$ and $y _1=1$
$$ \therefore \quad y-1=-\frac{2}{3}(x-1) $$
$\Rightarrow 2 x+3 y-5=0$
Now, equation of $A B$ is $4 x+5 y-20=0$ and equation of $B H$ is $2 x+3 y-5=0$
Solving these, we get point of intersection (i.e. coordinates of $B$ ).
$$ \begin{aligned} & 4 x+5 y-20=0 \\ & 4 x+6 y-10=0 \end{aligned} \Rightarrow y=-10 $$
On substituting $y=-10$ in $2 x+3 y-5=0$, we get $x=\frac{35}{2}$
$$ \therefore \quad B \frac{35}{2},-10 $$
Solving $4 x+5 y-20=0$ and $3 x-2 y+6=0$, we get coordinate of $A$.
$$ \begin{gathered} \left.\begin{array}{rl} 12 x+15 y-60 & =0 \\ 12 x-8 y+24=0 \end{array} } \Rightarrow 23 y=84 \\ \Rightarrow \quad y=\frac{84}{23} \Rightarrow x=\frac{10}{23} \\ \therefore \quad A \frac{10}{23}, \frac{84}{23} \end{gathered} $$
Now, slope of $A H=\frac{y _2-y _1}{x _2-x _1}=\frac{\frac{84}{23}-1}{\frac{10}{23}-1}=\frac{61}{-13}$.
$\because B C$ is perpendicular to $A H$. $\therefore$ Slope of $B C$ is $\frac{13}{61}$
$$ \because m _{B C}=-\frac{1}{m _{A H}} $$
Now, equation of line $B C$ is given by $y-y _1=m\left(x-x _1\right)$, where $\left(x _1, y _1\right)$ are coordinates of $B$.
$$ \begin{array}{ll} \therefore & y-(-10)=\frac{13}{61} \quad x-\frac{35}{2} \\ \Rightarrow & y+10=\frac{13}{61 \times 2}(2 x-35) \\ \Rightarrow & 122 y+1220=26 x-455 \\ \Rightarrow & 26 x-122 y-1675=0 \end{array} $$
