Properties of Triangles 3 Question 15
15. Circle with radii 3,4 and 5 touch each other externally, if
(2005, 2M)
Show Answer
Answer:
Correct Answer: 15.
Solution:
- Since, the circles with radii 3,4 and 5 touch each other externally and
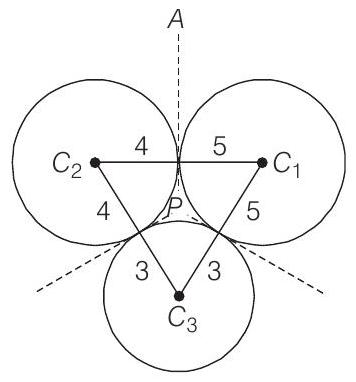
Thus, distance of point
i.e.
where,
Hence,






