Properties of Triangles 3 Question 13
13. The sides of a triangle inscribed in a given circle subtend angles
Show Answer
Answer:
Correct Answer: 13.
Solution:
- Since, sides of a triangle subtends
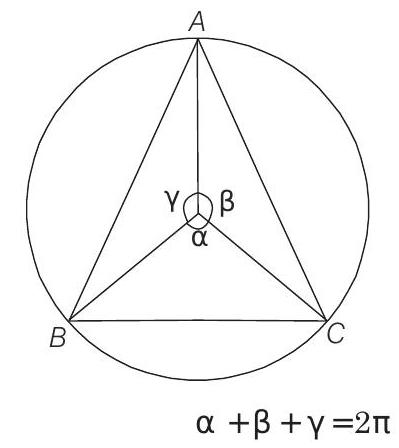
As we know that,
AM is minimum, when
or






