Properties of Triangles 3 Question 10
10. In a
(2016 Adv.)
(a) area of the
(b) the radius of circumcircle of the
Show Answer
Answer:
Correct Answer: 10.
Solution:
- Given a
and
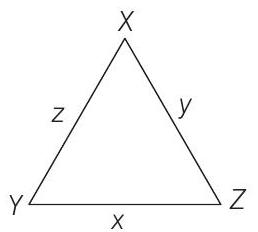
or
and
Now,
[Heron’s formula]
Also,
and
Now,
[from Eq. (ii)]
(a)
(b) Radius of circumcircle
(c) Since,
(d)






