Properties of Triangles 3 Question 1
1. Two vertices of a triangle are
(2019 Main, 10 Jan II)
(a) Fourth
(b) Third
(c) Second
(d) First
Show Answer
Answer:
Correct Answer: 1. (c)
Solution:
- Let
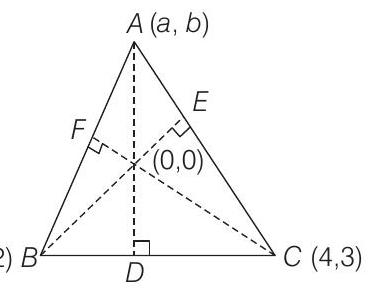
Also, let
Then,
[if two lines having slopes
From Eqs. (i) and (ii), we get
So, the third vertex






