Properties of Triangles 2 Question 3
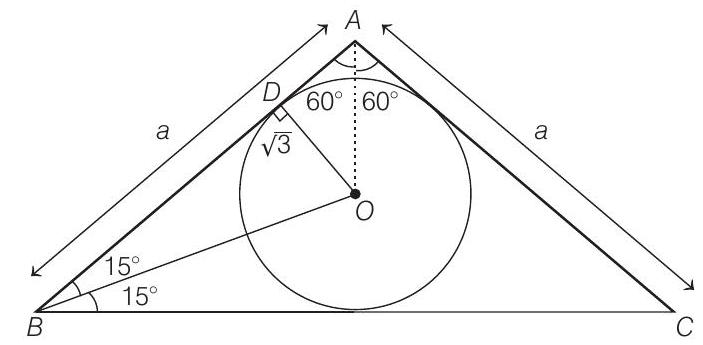
3. In radius of a circle which is inscribed in a isosceles triangle one of whose angle is
(2006, 2M)
(a)
(b)
(c)
(d) None of these
Show Answer
Answer:
Correct Answer: 3. (c)
Solution:
- Let
where,