Properties of Triangles 2 Question 17
17. Let
(2009)
Show Answer
Solution:
- In
When,
When,
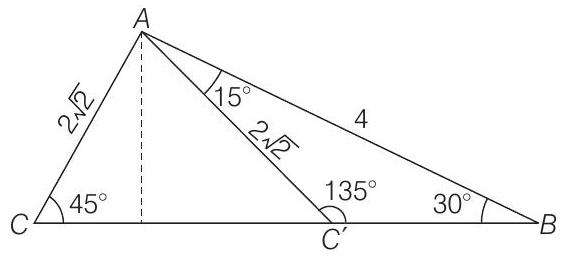
Area of
Area of
Difference of areas of triangle
Alternate Solution
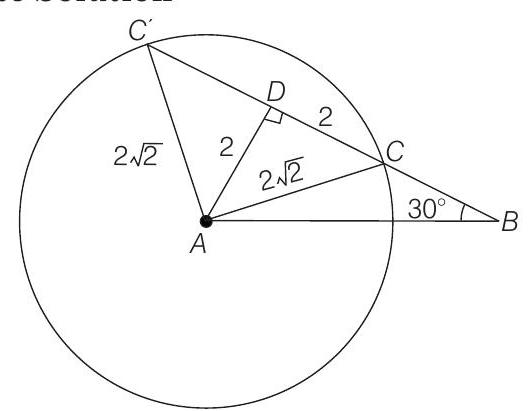
Here,
Difference of areas of






