Properties of Triangles 2 Question 12
12. In a triangle of base
(1991, 4M)
Show Answer
Solution:
- Let
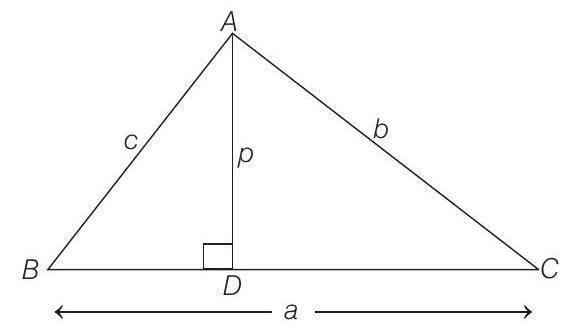
Area of
Also, area of






