SATHEE: Properties of Triangles 2 Question 10

Properties of Triangles 2 Question 10

10. Let $A, B, C$ be three angles such that $A = \frac{π}{4}$ and $\tan B, \tan C = p$ . Find all positive values of $p$ such that $A, B, C$ are the angles of triangle.

(1997C, 5M)

Show Answer

Solution:

Since, $A + B + C = π$

$\Rightarrow B + C = π - π / 4 = 3 π / 4$

$∴ 0 < B, C < 3 π / 4$

$[∵ A = π / 4$ , given $]$

Also, given $\tan B \cdot \tan C = p$

$\Rightarrow \frac{\sin B \cdot \sin C}{\cos B \cdot \cos C} = \frac{p}{1}$

$\Rightarrow \frac{\sin B \cdot \sin C + \cos B \cos C}{\sin B \cdot \sin C - \cos B \cdot \cos C} = \frac{p + 1}{p - 1}$

$\Rightarrow \frac{\cos (B - C)}{\cos (B + C)} = \frac{1 + p}{1 - p}$

$\Rightarrow \cos (B - C) = - \frac{(1 + p)}{\sqrt{2} (1 - p)}$

$[∵ B + C = 3 π / 4]$

Since, $B$ or $C$ can vary from 0 to $3 π / 4$

$\begin{array}{ll} ∴ & 0 \leq B - C < 3 π / 4 \\ \Rightarrow & - \frac{1}{\sqrt{2}} < \cos (B - C) \leq 1 \end{array}$

From Eqs. (ii) and (iii), $- \frac{1}{\sqrt{2}} < \frac{1 + p}{\sqrt{2} (p - 1)} \leq 1$

$\begin{aligned} \Rightarrow - \frac{1}{\sqrt{2}} < \frac{1 + p}{\sqrt{2} (p - 1)} and \frac{1 + p}{\sqrt{2} (p - 1)} \leq 1 \\ \Rightarrow \frac{1 + p}{p - 1} + 1 \geq 0 and \frac{1 + p - \sqrt{2} p + \sqrt{2}}{\sqrt{2} (p - 1)} \leq 0 \\ \Rightarrow \frac{2 p}{p - 1} \geq 0 and \frac{(1 - \sqrt{2}) p - \frac{1 + \sqrt{2}}{1 - \sqrt{2}}}{\sqrt{2} (p - 1)} \leq 0 \\ \Rightarrow \frac{2 p}{p - 1} > 0 and \frac{(p - (\sqrt{2} + 1)^{2})}{(p - 1)} \geq 0 \end{aligned}$

$\begin{aligned} \Rightarrow (p < 0 or p > 1) \\ and (p < 1 or p > (\sqrt{2} + 1)^{2}) \end{aligned}$

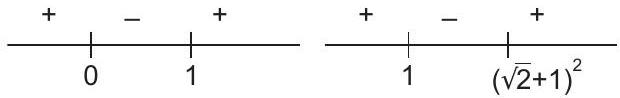
On combining above expressions, we get

$\begin{array}{ll} p < 0 or p \geq (\sqrt{2} + 1)^{2} \\ i.e. & p \in (- \infty, 0) \cup [(\sqrt{2} + 1)^{2}, \infty) \\ or & p \in (- \infty, 0) \cup [3 + 2 \sqrt{2}, \infty) \end{array}$