Properties of Triangles 1 Question 3
3. In a triangle, the sum of lengths of two sides is $x$ and the product of the lengths of the same two sides is $y$. If $x^{2}-c^{2}=y$, where $c$ is the length of the third side of the triangle, then the circumradius of the triangle is
(2019 Main, 11 Jan I)
(a) $\frac{c}{3}$
(b) $\frac{c}{\sqrt{3}}$
(c) $\frac{3}{2} y$
(d) $\frac{y}{\sqrt{3}}$
Show Answer
Answer:
Correct Answer: 3. (b)
Solution:
- We know that, $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2 R$ and given that, $a+b=x, a b=y$ and $x^{2}-c^{2}=y$
$$ \begin{array}{ll} \therefore & (a+b)^{2}-c^{2}=a b \\ \Rightarrow & a^{2}+b^{2}-c^{2}=-2 a b+a b \\ \Rightarrow & a^{2}+b^{2}-c^{2}=-a b \\ \Rightarrow & \frac{a^{2}+b^{2}-c^{2}}{2 a b}=\frac{-a b}{2 a b}=-\frac{1}{2} \end{array} $$
$\therefore \cos C=-\frac{1}{2} \Rightarrow C=120^{\circ}$
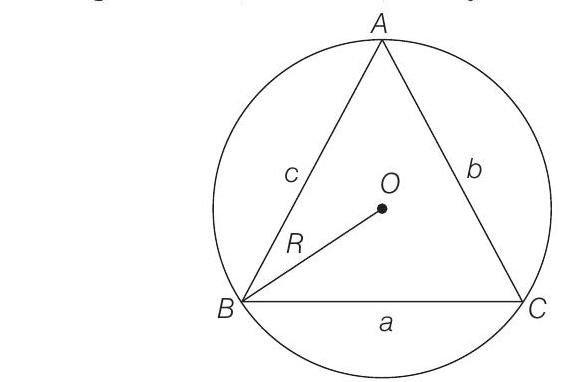
[using cosine rule, $\cos C=\frac{a^{2}+b^{2}-c^{2}}{2 a b}$ ]
Now, $\quad \frac{c}{\sin C}=2 R$
$$ \begin{array}{ll} \Rightarrow & R=\frac{1}{2} \frac{c}{\sin \left(120^{\circ}\right)}=\frac{c}{2} \frac{2}{\sqrt{3}} \\ \therefore & R=\frac{c}{\sqrt{3}} \end{array} $$
