Properties of Triangles 1 Question 21
21. In a $\triangle A B C$, the median to the side $B C$ is of length $\frac{1}{\sqrt{11-6 \sqrt{3}}}$ and it divides the $\angle A$ into angles $30^{\circ}$ and $45^{\circ}$. Find the length of the side $B C$.
$(1985,5 M)$
Show Answer
Solution:
- Let $A D$ be the median to the base $B C=a$ of $\triangle A B C$ and let $\angle A D C=\theta$, then
$$ \begin{aligned} \Rightarrow \quad \frac{a}{2}+\frac{a}{2} \cot \theta & =\frac{a}{2} \cot 30^{\circ}-\frac{a}{2} \cot 45^{\circ} \\ \cot \theta & =\frac{\sqrt{3}-1}{2} \end{aligned} $$
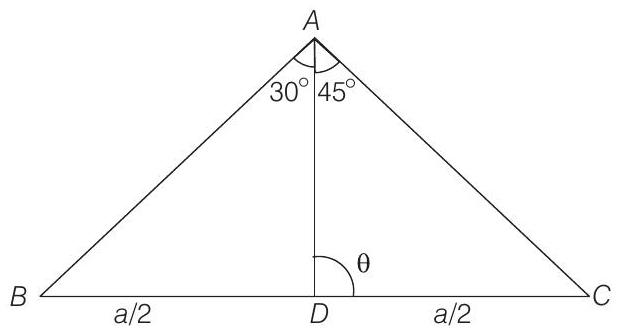
Applying sine rule in $\triangle A D C$, we get
$$ \frac{A D}{\sin \left(\pi-\theta-45^{\circ}\right)}=\frac{D C}{\sin 45^{\circ}} $$
$$ \begin{gathered} \Rightarrow \quad \frac{A D}{\sin \left(\theta+45^{\circ}\right)}=\frac{\frac{a}{2}}{\frac{1}{\sqrt{2}}} \\ \Rightarrow \quad A D=\frac{a}{\sqrt{2}}\left(\sin 45^{\circ} \cos \theta+\cos 45^{\circ} \sin \theta\right) \\ \Rightarrow \quad A D=\frac{a}{\sqrt{2}} \quad \frac{\cos \theta+\sin \theta}{\sqrt{2}}=\frac{a}{2}(\cos \theta+\sin \theta) \\ \Rightarrow \quad \frac{1}{\sqrt{11-6 \sqrt{3}}}=\frac{a}{2} \frac{\sqrt{3}-1}{\sqrt{8-2 \sqrt{3}}}+\frac{2}{\sqrt{8-2 \sqrt{3}}} \\ \Rightarrow \quad a=\frac{2 \sqrt{8-2 \sqrt{3}}}{(\sqrt{3}+1) \sqrt{11-6 \sqrt{3}}}=\frac{2 \sqrt{8-2 \sqrt{3}}}{\sqrt{(\sqrt{3}+1)^{2}} \sqrt{11-6 \sqrt{3}}} \\ =\frac{2 \sqrt{8-2 \sqrt{3}}}{\sqrt{(4+2 \sqrt{3})(11-6 \sqrt{3})}} \\ =\frac{2 \sqrt{8-2 \sqrt{3}}}{\sqrt{44-24 \sqrt{3}+22 \sqrt{3}-36}} \\ =2 \frac{\sqrt{8-2 \sqrt{3}}}{\sqrt{8-2 \sqrt{3}}}=2 \end{gathered} $$
