Properties of Triangles 1 Question 20
20. The sides of a triangle are three consecutive natural numbers and its largest angle is twice the smallest one. Determine the sides of the triangle.
(1991, 4M)
Show Answer
Solution:
- Let
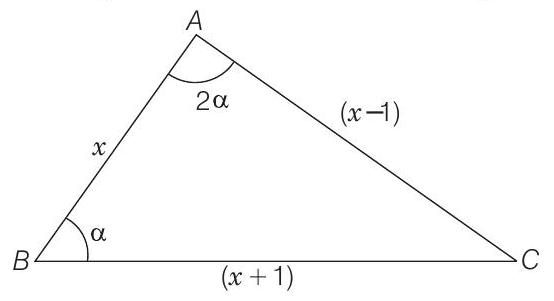
Then, by sine rule, we have
Also,
From Eqs. (i) and (ii),
Hence, the lengths of the sides of the triangle are 4, 5 and 6 units.






