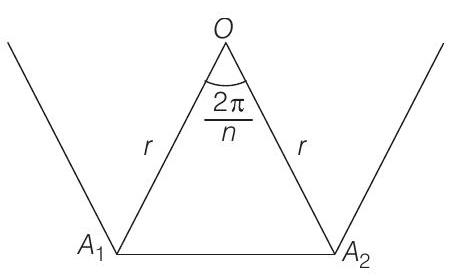
SATHEE: Properties of Triangles 1 Question 19

Properties of Triangles 1 Question 19

19. Let $A_{1}, A_{2}, \dots, A_{n}$ be the vertices of an $n$ -sided regular polygon such that $\frac{1}{A_{1} A_{2}} = \frac{1}{A_{1} A_{3}} + \frac{1}{A_{1} A_{4}}$ . Find the value of $n$ .

$(1994, 4$ M)

Show Answer

Answer:

Correct Answer: 19. 2

的 $∠ A = 75$

Solution:

Let $O$ be the centre and $r$ be the radius of the circle passing through the vertices $A_{1}, A_{2}, \dots, A_{n}$ .

Then,

$\begin{aligned} ∠ A_{1} O A_{2} & = \frac{2 π}{n} \\ O A_{1} & = O A_{2} = r \end{aligned}$

also

Again, by cos formula, we know that,

$\cos \frac{2 π}{n} = \frac{O A_{1}^{2} + O A_{2}^{2} - A_{1} A_{2}^{2}}{2 (O A_{1}) (O A_{2})}$

$\begin{aligned} \Rightarrow \cos \frac{2 π}{n} = \frac{r^{2} + r^{2} - A_{1} A_{2}^{2}}{2 (r) (r)} \\ \Rightarrow 2 r^{2} \cos \frac{2 π}{n} = 2 r^{2} - A_{1} A_{2}^{2} \\ \Rightarrow A_{1} A_{2}^{2} = 2 r^{2} - 2 r^{2} \cos \frac{2 π}{n} \\ \Rightarrow A_{1} A_{2}^{2} = 2 r^{2} 1 - \cos \frac{2 π}{n} \\ \Rightarrow A_{1} A_{2}^{2} = 2 r^{2} \cdot 2 \sin^{2} \frac{π}{n} \\ \Rightarrow A_{1} A_{2}^{2} = 4 r^{2} \sin^{2} \frac{π}{n} \\ \Rightarrow A_{1} A_{2} = 2 r \sin \frac{π}{n} \\ Similarly, A_{1} A_{3} = 2 r \sin \frac{2 π}{n} \\ and A_{1} A_{4} = 2 r \sin \frac{3 π}{n} \\ Since, \frac{1}{A_{1} A_{2}} = \frac{1}{A_{1} A_{3}} + \frac{1}{A_{1} A_{4}} \\ [given] \\ \Rightarrow \frac{1}{2 r \sin (π / n)} = \frac{1}{2 r \sin (2 π / n)} + \frac{1}{2 r \sin (3 π / n)} \\ \Rightarrow \frac{1}{\sin (π / n)} = \frac{1}{\sin (2 π / n)} + \frac{1}{\sin (3 π / n)} \\ \Rightarrow \frac{1}{\sin (π / n)} = \frac{\sin \frac{3 π}{n} + \sin \frac{2 π}{n}}{\sin (2 π / n) \sin (3 π / n)} \\ \Rightarrow \sin \frac{2 π}{n} \cdot \sin \frac{3 π}{n} = \sin \frac{π}{n} \sin \frac{3 π}{n} \\ + \sin \frac{π}{n} \cdot \sin \frac{2 π}{n} \\ \Rightarrow \sin \frac{2 π}{n} \sin \frac{3 π}{n} - \sin \frac{π}{n} = \sin \frac{π}{n} \cdot \sin \frac{3 π}{n} \\ \Rightarrow \sin \frac{2 π}{n} 2 \cos \frac{3 π + π}{2 n} \sin \frac{3 π - π}{2 n} \\ = \sin \frac{π}{n} \cdot \sin \frac{3 π}{n} \\ \Rightarrow 2 \sin \frac{2 π}{n} \cdot \cos \frac{2 π}{n} \cdot \sin \frac{π}{n} = \sin \frac{π}{n} \sin \frac{3 π}{n} \\ \Rightarrow 2 \sin \frac{2 π}{n} \cos \frac{2 π}{n} = \sin \frac{3 π}{n} \\ \Rightarrow \sin \frac{4 π}{n} = \sin \frac{3 π}{n} \\ \Rightarrow \frac{4 π}{n} = π - \frac{3 π}{n} \\ \Rightarrow \frac{7 π}{n} = π \\ \Rightarrow n = 7 \end{aligned}$