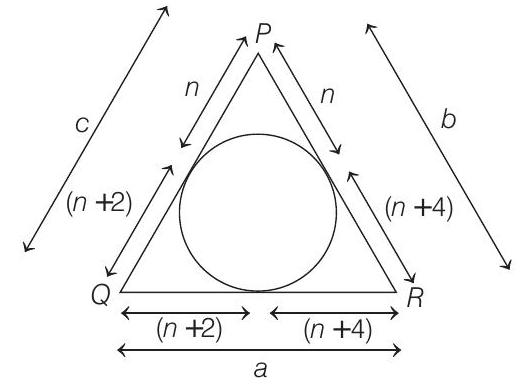
Properties of Triangles 1 Question 12
12. In a $\triangle P Q R, P$ is the largest angle and $\cos P=\frac{1}{3}$. Further in circle of the triangle touches the sides $P Q, Q R$ and $R P$ at $N, L$ and $M$ respectively, such that the lengths of $P N, Q L$ and $R M$ are consecutive even integers. Then, possible length(s) of the side(s) of the triangle is (are)
(2017 Main)
(a) 16
(b) 18
(c) 24
(d) 22
Show Answer
Answer:
Correct Answer: 12. (b)
Solution:
- PLAN Whenever cosine of angle and sides are given or to find out, we should always use Cosine law.
i.e. $\cos A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}, \quad \cos B=\frac{a^{2}+c^{2}-b^{2}}{2 a c}$
and $\cos C=\frac{a^{2}+b^{2}-c^{2}}{2 a b}$
$\therefore \quad \cos P=\frac{b^{2}+c^{2}-a^{2}}{2 b c}$
$\Rightarrow \quad \frac{1}{3}=\frac{(2 n+4)^{2}+(2 n+2)^{2}-(2 n+6)^{2}}{2(2 n+4)(2 n+2)}$
$\because \cos p=\frac{1}{3}$, given
$\Rightarrow \quad \frac{4 n^{2}-16}{8(n+1)(n+2)}=\frac{1}{3}$
$\Rightarrow \quad \frac{n^{2}-4}{2(n+1)(n+2)}=\frac{1}{3}$
$\Rightarrow \quad \frac{(n-2)}{2(n+1)}=\frac{1}{3}$
$\Rightarrow \quad 3 n-6=2 n+2 \Rightarrow \quad n=8$
$\therefore \quad$ Sides are $(2 n+2),(2 n+4),(2 n+6)$, i.e. $18,20,22$.
