Properties of Triangles 1 Question 10
10. If in a $\triangle P Q R, \sin P, \sin Q, \sin R$ are in $AP$, then
(a) the altitudes are in $AP$
(1998, 2M)
(b) the altitudes are in HP
(c) the medians are in GP
(d) the medians are in AP
Show Answer
Answer:
Correct Answer: 10. (b, c)
Solution:
- By the law of sine rule,
$$ \frac{a}{\sin P}=\frac{b}{\sin Q}=\frac{c}{\sin R}=k $$
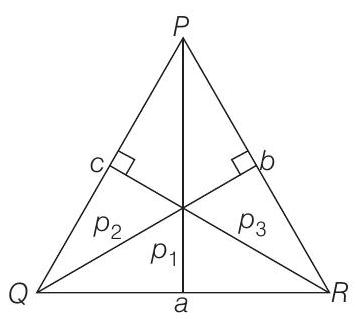
Also,
$$ \frac{1}{2} a p _1=\Delta $$
$$ \begin{array}{ll} \Rightarrow & \frac{2 \Delta}{a}=p _1 \\ \Rightarrow & p _1=\frac{2 \Delta}{k \sin P} \end{array} $$
Similarly, $\quad p _2=\frac{2 \Delta}{k \sin Q}$ and $p _3=\frac{2 \Delta}{k \sin R}$
Since, $\sin P, \sin Q$ and $\sin R$ are in AP, hence $p _1, p _2, p _3$ are in HP.
