Probability 4 Question 8
8. A ball is drawn at random from box I and transferred to box II. If the probability of drawing a red ball from box I, after this transfer, is
(a)
(b)
(c)
(d)
Passage II
Let
(2011)
Show Answer
Answer:
Correct Answer: 8. (d)
Solution:
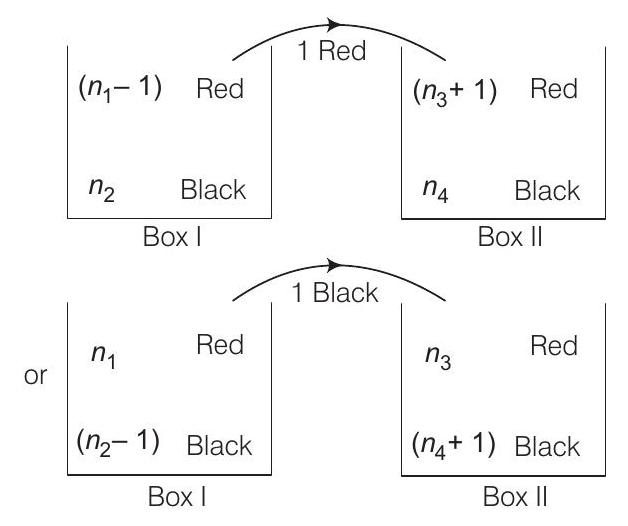
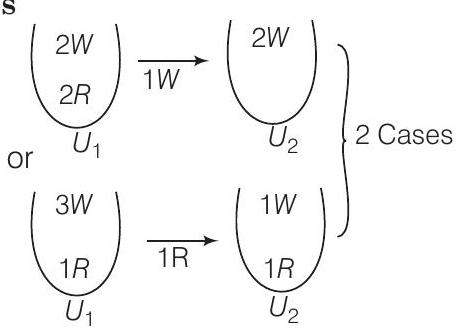
Clearly, options (c) and (d) satisfy.
Passage II
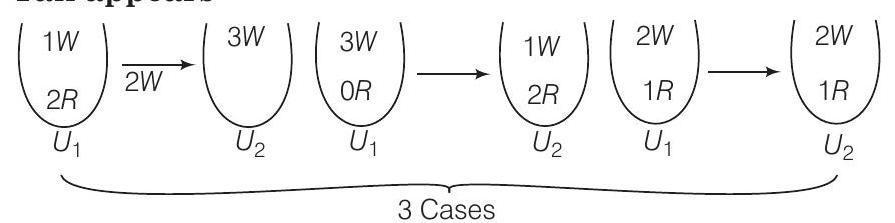
Head appears
Tail appears