Probability 4 Question 4
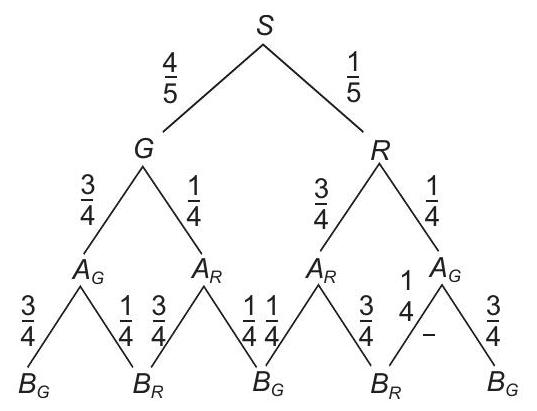
4. A signal which can be green or red with probability
(2010)
(a)
(b)
(c)
(d)
Objective Question II
(One or more than one correct option)
Show Answer
Answer:
Correct Answer: 4. (c)
Solution:
- From the tree diagram, it follows that