Probability 3 Question 23
23. Let
(2011)
(a)
(b)
(c)
(d)
Show Answer
Solution:
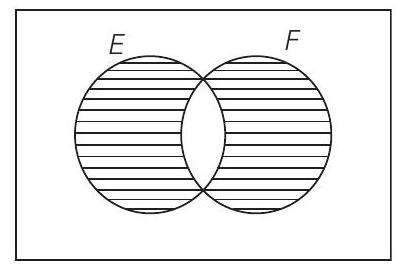
[i.e. only
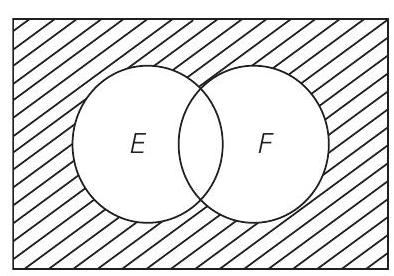
Neither of them occurs
From Eq. (i),
From Eq. (ii),
From Eqs. (iii) and (iv),






