Parabola 3 Question 2
2. If $x+y=k$ is normal to $y^{2}=12 x$, then $k$ is
(a) 3
$(2000,2 M)$
(b) 9
(c) -9
(d) -3
Match the Columns
Show Answer
Answer:
Correct Answer: 2. (b)
Solution:
- Given, equation of parabola is $x^{2}=4 y$
and the chord is $x-\sqrt{2} y+4 \sqrt{2}=0$
From Eqs. (i) and (ii), we have
$$ \begin{aligned} & & {[\sqrt{2}(y-4)]^{2} } & =4 y \\ \Rightarrow & & 2(y-4)^{2} & =4 y \\ \Rightarrow & & (y-4)^{2} & =2 y \\ \Rightarrow & & y^{2}-8 y+16 & =2 y \\ \Rightarrow & & y^{2}-10 y+16 & =0 \end{aligned} $$
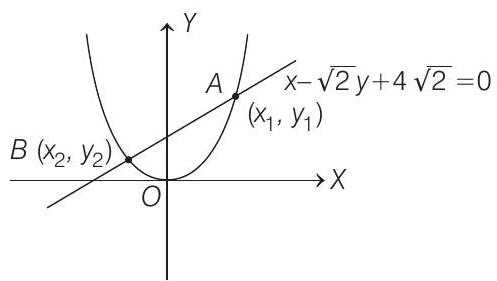
Let the roots of Eq. (iii) be $y _1$ and $y _2$ Then,
$$ y _1+y _2=10 \text { and } y _1 y _2=16 $$
Again from Eqs. (i) and (ii), we have
$$ \begin{aligned} x^{2} & =4 \frac{x}{\sqrt{2}}+4 \\ \Rightarrow \quad x^{2}-2 \sqrt{2} x-16 & =0 \end{aligned} $$
Let the roots of Eq. (v) be $x _1$ and $x _2$
Then, $\quad x _1+x _2=2 \sqrt{2}$
and $\quad x _1 x _2=-16$
Clearly, length of the chord $A B$
$$ \begin{aligned} & =\sqrt{\left(x _1-x _2\right)^{2}+\left(y _1-y _2\right)^{2}} \\ & =\sqrt{\left(x _1+x _2\right)^{2}-4 x _1 x _2+\left(y _1+y _2\right)^{2}-4 y _1 y _2} \\ & =\sqrt{8+64+100-64} \quad\left[\because(a-b)^{2}=(a+b)^{2}-4 a b\right] \\ & =\sqrt{108}=6 \sqrt{3} \quad \text { [from Eqs. (iv) and (vi)] } \end{aligned} $$






