Parabola 3 Question 11
11. Find the equation of the normal to the curve $x^{2}=4 y$ which passes through the point $(1,2)$.
(1984, 4M)
Show Answer
Answer:
Correct Answer: 11. $x+y=3$
Solution:
- Let the equation of chord $O P$ be $y=m x$.
Then, equation of chord will be $y=-\frac{1}{m} x$ and
$P$ is point of intersection of $y=m x$ and $y^{2}=4 x$ is $\frac{4}{m^{2}}, \frac{4}{m}$ and $Q$ is point intersection of $y=-\frac{1}{m} x$ and $y^{2}=4 x$ is $\left(4 m^{2},-4 m\right)$.
Now, equation of $P Q$ is
$$ y+4 m=\frac{\frac{4}{m}+4 m}{\frac{4}{m^{2}}-4 m^{2}}\left(x-4 m^{2}\right) $$
$$ \begin{array}{lc} \Rightarrow & y+4 m=\frac{m}{1-m^{2}}\left(x-4 m^{2}\right) \\ \Rightarrow & \left(1-m^{2}\right) y+4 m-4 m^{3}=m x-4 m^{3} \\ \Rightarrow & m x-\left(1-m^{2}\right) y-4 m=0 \end{array} $$
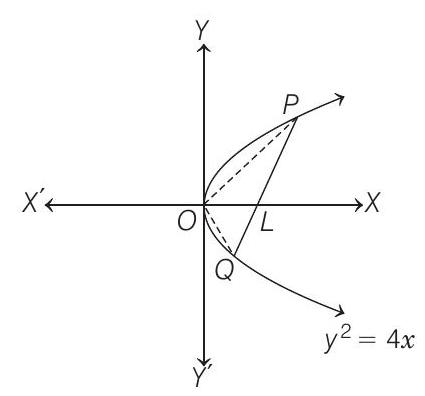
This line meets $X$-axis, where $y=0$
i.e. $x=4 \Rightarrow O L=4$ which is constant as independent of $m$.
Again, let $(h, k)$ be the mid-point of $P Q$. Then,
$$ \begin{array}{rlrl} & & h=\frac{4 m^{2}+\frac{4}{m^{2}}}{2} \\ \text { and } & k & =\frac{\frac{4}{m}-4 m}{2} \\ \Rightarrow & & h=2 & m^{2}+\frac{1}{m^{2}} \\ \text { and } & k & =2 \frac{1}{m}-m \\ \Rightarrow & h & =2 & m-\frac{1}{m}^{2}+2 \\ \text { and } & k & =2 \frac{1}{m}-m \end{array} $$
Eliminating $m$, we get
$$ 2 h=k^{2}+8 $$
or $y^{2}=2(x-4)$ is required equation of locus.
