SATHEE: Parabola 3 Question 10

Parabola 3 Question 10

10. Three normals are drawn from the point $(c, 0)$ to the curve $y^{2} = x$ . Show that $c$ must be greater than $\frac{1}{2}$ . One normal is always the $X$ -axis. Find $c$ for which the other two normals are perpendicular to each other.

(1991, 4M)

Show Answer

Answer:

Correct Answer: 10. $\frac{3}{4}$

Solution:

Let $A (t_{1}^{2}, 2 t_{1})$ and $B (t_{2}^{2}, 2 t_{2})$ be coordinates of the end points of a chord of the parabola $y^{2} = 4 x$ having slope 2 .

Now, slope of $A B$ is

$m = \frac{2 t_{2} - 2 t_{1}}{t_{2}^{2} - t_{1}^{2}} = \frac{2 (t_{2} - t_{1})}{(t_{2} - t_{1}) (t_{2} + t_{1})} = \frac{2}{t_{2} + t_{1}}$

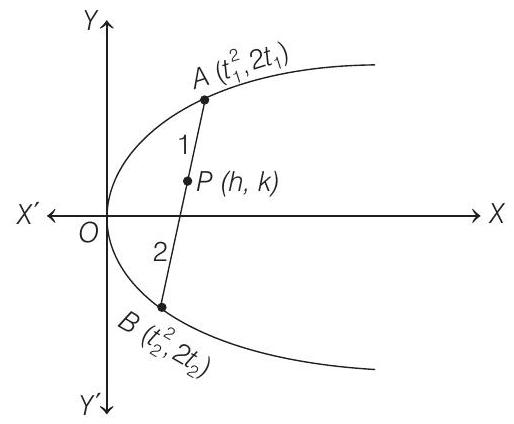
But

$\begin{matrix} m = 2 \\ 2 = \frac{2}{t_{2} + t_{1}} \\ t_{1} + t_{2} = 1 \end{matrix}$

[given]

Let $P (h, k)$ be a point on $A B$ such that, it divides $A B$ internally in the ratio $1 : 2$ .

Then, $h = \frac{2 t_{1}^{2} + t_{2}^{2}}{2 + 1}$ and $k = \frac{2 (2 t_{1}) + 2 t_{2}}{2 + 1}$

$\begin{aligned} \Rightarrow 3 h = 2 t_{1}^{2} + t_{2}^{2} \\ and 3 k = 4 t_{1} + 2 t_{2} \end{aligned}$

On substituting value of $t_{1}$ from Eq. (i) in Eq. (iii)

$\begin{aligned} 3 k & = 4 (1 - t_{2}) + 2 t_{2} \\ \Rightarrow & 3 k & = 4 - 2 t_{2} \\ \Rightarrow & t_{2} = 2 - \frac{3 k}{2} \end{aligned}$

On substituting $t_{1} = 1 - t_{2}$ in Eq. (ii), we get

$\begin{aligned} 3 h = 2 {(1 - t_{2})}^{2} + t_{2}^{2} \\ = 2 (1 - 2 t_{2} + t_{2}^{2}) + t_{2}^{2} \\ = 3 t_{2}^{2} - 4 t_{2} + 2 = 3 t_{2}^{2} - \frac{4}{3} t_{2} + \frac{2}{3} \\ = 3 t_{2} - {\frac{2}{3}}^{2} + \frac{2}{3} - \frac{4}{9} = 3 t_{2} - {\frac{2}{3}}^{2} + \frac{2}{3} \\ \Rightarrow 3 h - \frac{2}{3} = 3 t_{2} - {\frac{2}{3}}^{2} \\ \Rightarrow 3 h - \frac{2}{9} = 32 - \frac{3 k}{2} - {\frac{2}{3}}^{2} [from Eq. (iv)] \\ \Rightarrow 3 h - \frac{2}{9} = 3 \frac{4}{3} - {\frac{3 k}{2}}^{2} \\ \Rightarrow h - \frac{2}{9} = \frac{9}{4} k - {\frac{8}{9}}^{2} \\ \Rightarrow k - {\frac{8}{9}}^{2} = \frac{4}{9} h - \frac{2}{9} \end{aligned}$