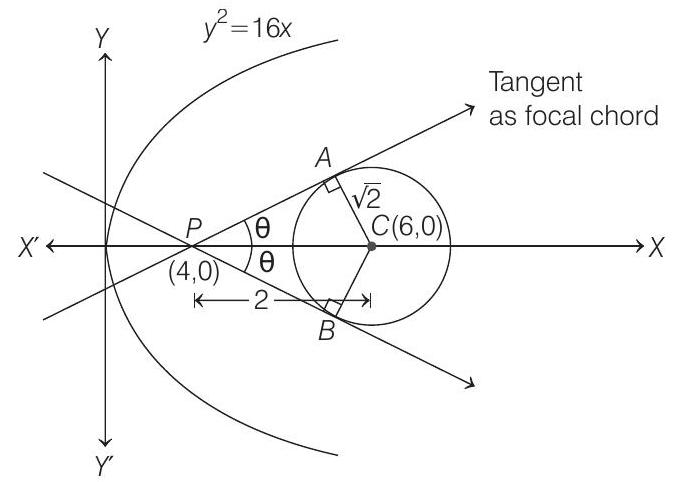
Parabola 2 Question 32
11. The focal chord to
(2003, 1M)
(a)
(b)
(c)
(d)
Show Answer
Solution:
- Here, the focal chord of
Now, tangents are drawn from
Since,