Parabola 2 Question 28
7. The radius of a circle having minimum area, which touches the curve $y=4-x^{2}$ and the lines $y=|x|$, is
(a) $2(\sqrt{2}+1)$
(b) $2(\sqrt{2}-1)$
(c) $4(\sqrt{2}-1)$
(d) $4(\sqrt{2}+1)$
(2017 Main)
Show Answer
Answer:
Correct Answer: 7. (c)
Solution:
- Let the radius of circle with least area be $r$.
Then, then coordinates of centre $=(0,4-r)$.
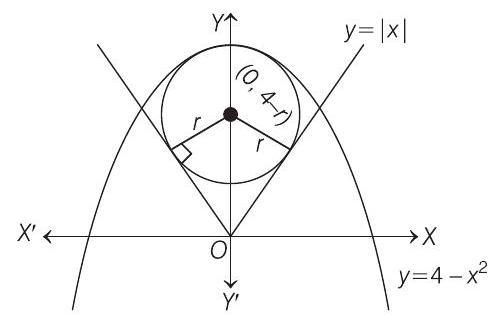
Since, circle touches the line $y=x$ in first quadrant
$\therefore\left|\frac{0-(4-r)}{\sqrt{2}}\right|=r \Rightarrow r-4= \pm r \sqrt{2}$
$\Rightarrow \quad r=\frac{4}{\sqrt{2}+1}$ or $\frac{4}{1-\sqrt{2}}$
But $r \neq \frac{4}{1-\sqrt{2}}$
$$ \because \frac{4}{1-\sqrt{2}}<0 $$
$\therefore \quad r=\frac{4}{\sqrt{2}+1}=4(\sqrt{2}-1)$
