Parabola 2 Question 21
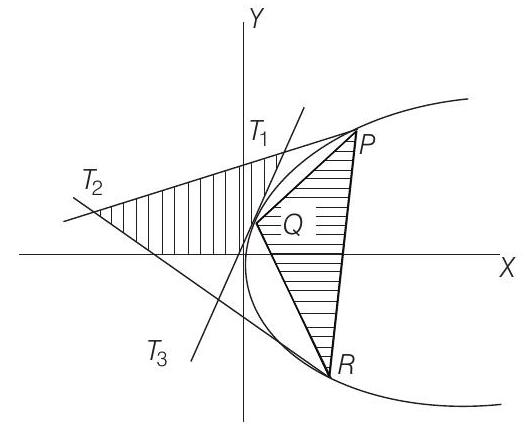
21. Consider the parabola $y^{2}=8 x$. Let $\Delta _1$ be the area of the triangle formed by the end points of its latusrectum and the point $P \frac{1}{2}, 2$ on the parabola and $\Delta _2$ be the area of the triangle formed by drawing tangents at $P$ and at the end points of the latusrectum. Then, $\frac{\Delta _1}{\Delta _2}$ is
(2011)
Show Answer
Solution:
- As, we know area of $\Delta$ formed by three points on parabola is twice the area of $\Delta$ formed by corresponding tangents i.e. area of $\triangle P Q R=2$ area of $\Delta T _1 T _2 T _3$.
$\therefore \quad \Delta _1=2 \Delta _2$ or $\frac{\Delta _1}{\Delta _2}=2$
Topic 3 Equation of Normal and Properties






