Parabola 2 Question 20
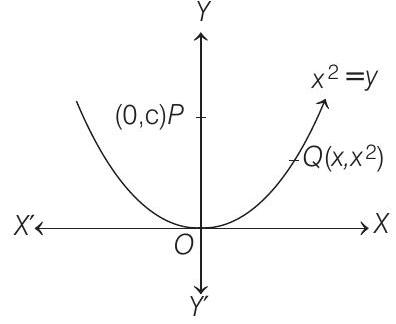
20. Find the shortest distance of the point $(0, c)$ from the parabola $y=x^{2}$, where $0 \leq c \leq 5$.
$(1982,2 M)$
Integer Answer Type Question
Show Answer
Solution:
- Let the point $Q\left(x, x^{2}\right)$ on $x^{2}=y$ whose distance from $(0, c)$ is minimum.
Now, $P Q^{2}=x^{2}+\left(x^{2}-c\right)^{2}$
$$ \text { Let } \begin{aligned} f(x) & =x^{2}+\left(x^{2}-c\right)^{2} \\ f^{\prime}(x) & =2 x+2\left(x^{2}-c\right) \cdot 2 x \\ & =2 x\left(1+2 x^{2}-2 c\right)=4 x \quad x^{2}-c+\frac{1}{2} \end{aligned} $$
$$ =4 x \quad x-\sqrt{c-\frac{1}{2}} \quad x+\sqrt{c-\frac{1}{2}}, \quad \text { when } c>\frac{1}{2} $$
For maxima, put $f^{\prime}(x)=0$
$$ 4 x x^{2}-c+\frac{1}{2}=0 \Rightarrow x=0, x= \pm \sqrt{c-\frac{1}{2}} $$
Now,
$$ f^{\prime \prime}(x)=4 \quad x^{2}-c+\frac{1}{2}+4 x[2 x] $$
At
$$ x= \pm \sqrt{c-\frac{1}{2}} $$
$f^{\prime \prime}(x) \geq 0$. $\therefore f(x)$ is minimum.
Hence, minimum value of $f(x) \neq P Q \mid$
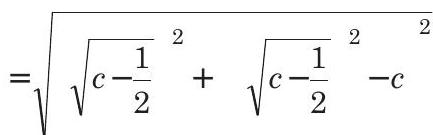
$$ \begin{aligned} & =\sqrt{c-\frac{1}{2}+c-\frac{1}{2}-c^{2}}=\sqrt{c-\frac{1}{4}}, \frac{1}{2} \leq c \leq 5 \end{aligned} $$






