Parabola 1 Question 7
7. Axis of a parabola is $y=x$ and vertex and focus are at a distance $\sqrt{2}$ and $2 \sqrt{2}$ respectively from the origin. Then, equation of the parabola is
(2006, 3M)
(a) $(x-y)^{2}=8(x+y-2)$
(b) $(x+y)^{2}=2(x+y-2)$
(c) $(x-y)^{2}=4(x+y-2)$
(d) $(x+y)^{2}=2(x-y+2)$
Show Answer
Answer:
Correct Answer: 7. (a)
Solution:
- Since, distance of vertex from origin is $\sqrt{2}$ and focus is $2 \sqrt{2}$.
$\therefore V(1,1)$ and $F(2,2)$ (i.e. lying on $y=x$ )
where, length of latusrectum
$$ =4 a=4 \sqrt{2} \quad[\because a=\sqrt{2}] $$
$\therefore$ By definition of parabola
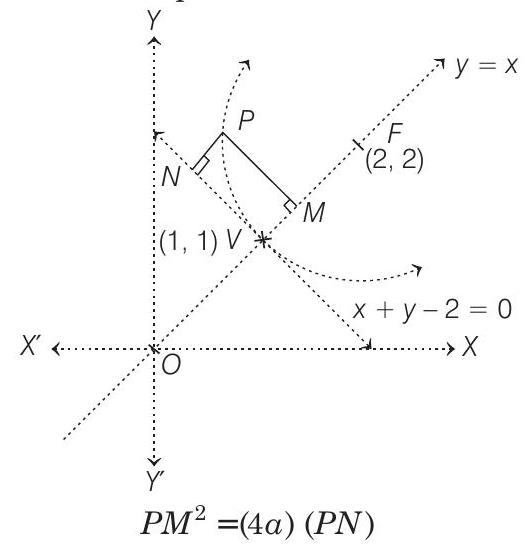
where, $P N$ is length of perpendicular upon $x+y-2=0$, i.e. tangent at vertex
$$ \begin{array}{ll} \Rightarrow & \frac{(x-y)^{2}}{2}=4 \sqrt{2} \quad \frac{x+y-2}{\sqrt{2}} \\ \Rightarrow & (x-y)^{2}=8(x+y-2) \end{array} $$






