Parabola 1 Question 6
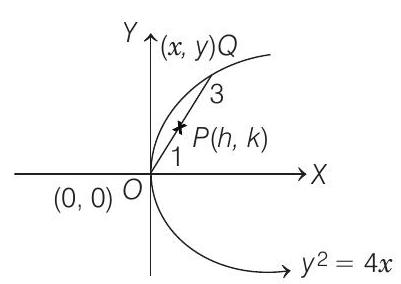
6. Let $(x, y)$ be any point on the parabola $y^{2}=4 x$. Let $P$ be the point that divides the line segment from $(0,0)$ to $(x, y)$ in the ratio $1: 3$. Then, the locus of $P$ is
(2011)
(a) $x^{2}=y$
(b) $y^{2}=2 x$
(c) $y^{2}=x$
(d) $x^{2}=2 y$
Show Answer
Answer:
Correct Answer: 6. (a)
Solution:
- By section formula,
$$ \begin{array}{ll} & h=\frac{x+0}{4}, k=\frac{y+0}{4} \\ & x=4 h, y=4 k \\ \underset{(0,0) O}{ } y^{2}=4 x \end{array} $$
Substituting in $y^{2}=4 x$,
$$ \begin{array}{rlrl} & & (4 k)^{2}=4(4 h) \\ \Rightarrow & k^{2}=h \end{array} $$
or $y^{2}=x$ is required locus.






