Parabola 1 Question 2
2. A circle cuts a chord of length $4 a$ on the $X$-axis and passes through a point on the $Y$-axis, distant $2 b$ from the origin. Then, the locus of the centre of this circle, is
(2019 Main, 11 Jan, II)
(a) a parabola
(b) an ellipse
(c) a straight line
(d) a hyperbola
Show Answer
Answer:
Correct Answer: 2. (a)
Solution:
- According to given information, we have the following figure.
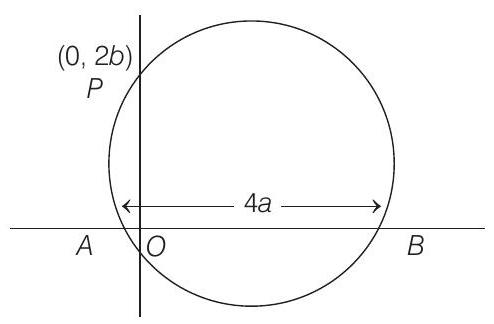
Let the equation of circle be
$$ x^{2}+y^{2}+2 g x+2 f y+c=0 $$
According the problem,
$$ 4 a=2 \sqrt{g^{2}-c} $$
$[\because$ The length of intercepts made by the circle $x^{2}+y^{2}+2 g x+2 f y+c=0$
$$ \text { with } \left.X \text {-axis is } 2 \sqrt{g^{2}-c}\right] $$
Also, as the circle is passing through $P(0,2 b)$
$$ \begin{array}{lrr} \therefore & 0+4 b^{2}+0+4 b f+c=0 & \text { [using Eq. (i)] } \\ \Rightarrow & 4 b^{2}+4 b f+c=0 & \ldots \text { (iii) } \end{array} $$
Eliminating ’ $c$ ’ from Eqs. (ii) and (iii), we get
$$ \begin{aligned} & 4 b^{2}+4 b f+g^{2}-4 a^{2}=0 \\ & {\left[\because 4 a=2 \sqrt{g^{2}-c} \Rightarrow c=g^{2}-4 a^{2}\right] } \end{aligned} $$
So, locus of $(-g,-f)$ is
$$ \begin{array}{rlrl} & & 4 b^{2}-4 b y+x^{2}-4 a^{2}=0 \\ \Rightarrow & x^{2}=4 b y+4 a^{2}-4 b^{2} \end{array} $$
which is a parabola.






