Parabola 1 Question 13
13. Let the curve $C$ be the mirror image of the parabola $y^{2}=4 x$ with respect to the line $x+y+4=0$. If $A$ and $B$ are the points of intersection of $C$ with the line $y=-5$, then the distance between $A$ and $B$ is
(2015 Adv.)
Show Answer
Answer:
Correct Answer: 13. (4)
Solution:
- Let $P\left(t^{2}, 2 t\right)$ be a point on the curve $y^{2}=4 x$, whose image is $Q(x, y)$ on $x+y+4=0$, then
$$ \begin{aligned} & & \frac{x-t^{2}}{1} & =\frac{y-2 t}{1}=\frac{-2\left(t^{2}+2 t+4\right)}{1^{2}+1^{2}} \\ \Rightarrow & & x & =-2 t-4 \\ \text { and } & & y & =-t^{2}-4 \end{aligned} $$
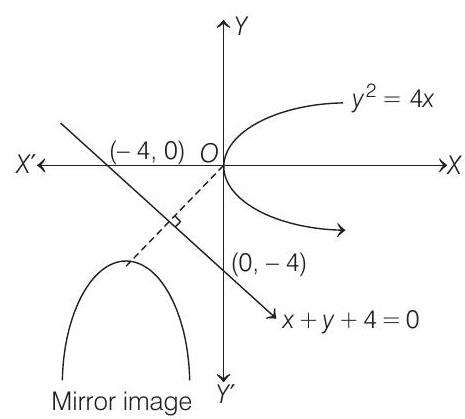
Now, the straight line $y=-5$ meets the mirror image.
$$ \begin{array}{lc} \therefore & -t^{2}-4=-5 \\ \Rightarrow & t^{2}=1 \\ \Rightarrow & t= \pm 1 \end{array} $$
Thus, points of intersection of $A$ and $B$ are $(-6,-5)$ and $(-2,-5)$.
$\therefore$ Distance, $A B=\sqrt{(-2+6)^{2}+(-5+5)^{2}}=4$






