Limit Continuity and Differentiability 4 Question 10
10. A discontinuous function
Analytical & Descriptive Questions
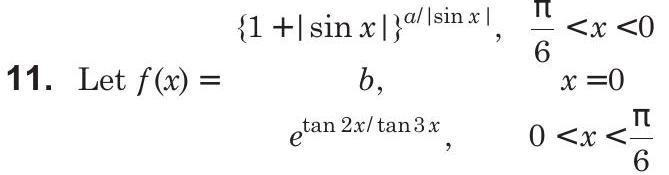
Determine
(1994, 4M)
Show Answer
Answer:
Correct Answer: 10.
Solution:
We know that,
Thus, the function is defined in the interval.
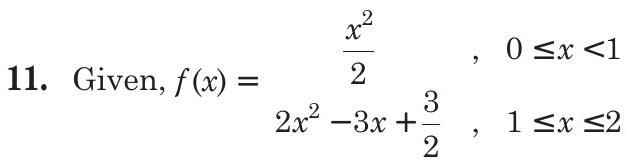
Clearly, RHL (at
On differentiating Eq. (i), we get
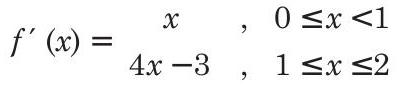
Clearly, RHL (at
and LHL (at
Also,
Thus,
Again, differentiating Eq. (ii), we get
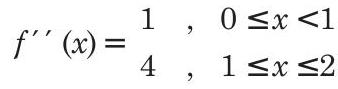
Clearly, RHL (at
Thus,
or






