Limit Continuity and Differentiability 2 Question 4
4. For each
(2019 Main, 10 Jan I)
(a) equals 0
(b) does not exist
(c) equals -1
(d) equals 1
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- Here,
Taking log on both sides, we get
Converting summation into definite integration, we get
Using Newton-Leibnitz formula, we get
Here, at
Now, sign scheme of
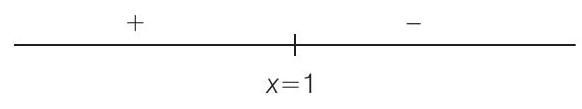
Since,
Also,
Also,






