Inverse Circular Functions 2 Question 11
11. Let
(Here, the inverse trigonometric function
(2018 Adv.)
| List I | List II | ||
|---|---|---|---|
| P. The range of |
1. | ||
| Q. | The range of |
2. | |
| The domain of contains |
3. | ||
| S. The domain of |
4. | ||
| 5. |
The correct option is
(a)
(b)
(c)
(d)
Numerical Value Based
Show Answer
Answer:
Correct Answer: 11. (c)
Solution:
- We have,
and
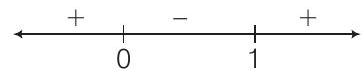
Now,
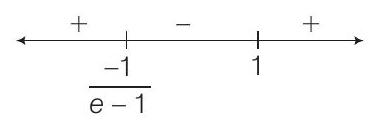
Also,
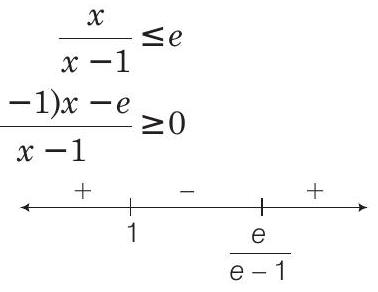
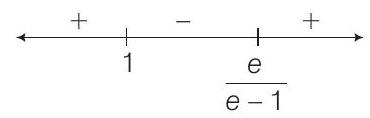
So,
and Range of
Range of
Now,






