SATHEE: Indefinite Integration 3 Question 21

Indefinite Integration 3 Question 21

21. If ’ $f$ ’ is a continuous function with $\int_{0}^{x} f (t) d t \to \infty$ as $| x | \to \infty$ , then show that every line $y = m x$ intersects the curve $y^{2} + \int_{0}^{x} f (t) d t = 2$

$(1991, 2 M)$

Show Answer

Solution:

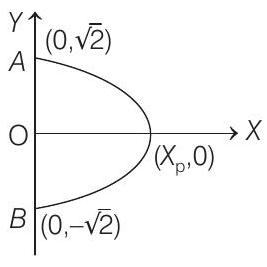
Since, $f$ is continuous function and $\int_{0}^{x} f (t) d t \to \infty$ , as $| x | \to \infty$ . To show that every line $y = m x$ intersects the curve $y^{2} + \int_{0}^{x} f (t) d t = 2$

At $x = 0, y = \pm \sqrt{2}$

Hence, $(0, \sqrt{2}), (0, - \sqrt{2})$ are the point of intersection of the curve with the $Y$ -axis. As $x \to \infty, \int_{0}^{x} f (t) d t \to \infty$ for a particular $x$ (say $x_{n}$ ), then $\int_{0}^{x} f (t) d t = 2$ and for this value of $x, y = 0$

The curve is symmetrical about $X$ -axis.

Thus, we have that there must be some $x$ , such that $f (x_{n}) = 2$ .

Thus, $y = m x$ intersects this closed curve for all values of $m$ .

पिछला

अगला

गोपनीयता नीति

द्वारा संचालित Prutor@IITK

sathee@iitk.ac.in

SATHEE का मीडिया कवरेज

खेल स्टोर

ऐप स्टोर

Ask SATHEE

Welcome to SATHEE !
Select from 'Menu' to explore our services, or ask SATHEE to get started. Let's embark on this journey of growth together! 🌐📚🚀🎓

I'm relatively new and can sometimes make mistakes.
If you notice any error, such as an incorrect solution, please use the thumbs down icon to aid my learning.
To begin your journey now, click on "I understand".

Indefinite Integration 3 Question 21

21. If ’ f ’ is a continuous function with ∫0xf(t)dt→∞ as |x|→∞, then show that every line y=mx intersects the curve y2+∫0xf(t)dt=2

Solution:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

21. If ’ $f$ ’ is a continuous function with $\int_{0}^{x} f (t) d t \to \infty$ as $| x | \to \infty$ , then show that every line $y = m x$ intersects the curve $y^{2} + \int_{0}^{x} f (t) d t = 2$