Indefinite Integration 1 Question 34
35. The value of
(a)
(b)
(c)
(d)
Show Answer
Solution:
- It is a question of greatest integer function. We have, subdivide the interval
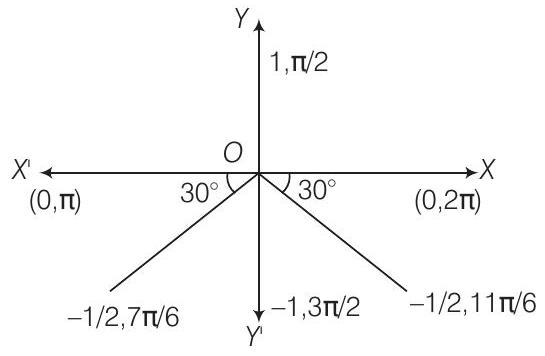
We know that,
Hence, we divide the interval






