Indefinite Integration 1 Question 12
13. Let
(2019 Main, 10 Jan I)
(a)
(b)
(c)
(d)
Show Answer
Solution:
- We have,
Graph of
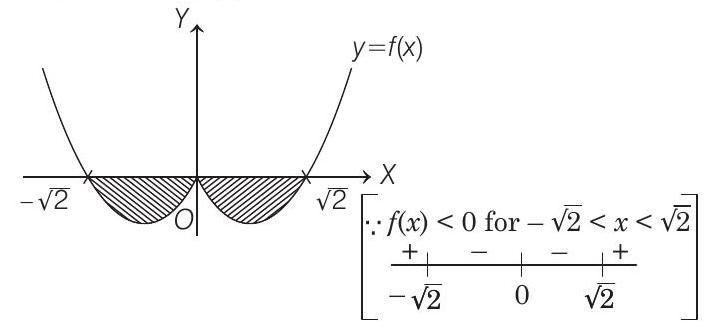
Note that the definite integral
But between






