Hyperbola 2 Question 12
12. Tangents are drawn to the hyperbola $\frac{x^{2}}{9}-\frac{y^{2}}{4}=1$, parallel to the straight line $2 x-y=1$. The points of contacts of the tangents on the hyperbola are
(2012)
(a) $\frac{9}{2 \sqrt{2}}, \frac{1}{\sqrt{2}}$
(b) $-\frac{9}{2 \sqrt{2}},-\frac{1}{\sqrt{2}}$
(c) $(3 \sqrt{3},-2 \sqrt{2)}$
(d) $(-3 \sqrt{3}, 2 \sqrt{2})$
Passage Based Problems
The circle $x^{2}+y^{2}-8 x=0$ and hyperbola $\frac{x^{2}}{9}-\frac{y^{2}}{4}=1$ intersect at the points $A$ and $B$.
(2010)
Show Answer
Answer:
Correct Answer: 12. (b)
Solution:
- PLAN Equation of tangent to $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ is $y=m x \pm \sqrt{a^{2} m^{2}-b^{2}}$
Description of Situation If two straight lines
$$ a _1 x+b _1 y+c _1=0 $$
and $a _2 x+b _2 y+c _2=0$ are identical. Then, $\frac{a _1}{a _2}=\frac{b _1}{b _2}=\frac{c _1}{c _2}$
Equation of tangent, parallel to $y=2 x-1$ is
$$ \begin{array}{rlrl} & & y & =2 x \pm \sqrt{9(4)-4} \\ \therefore & y & =2 x \pm \sqrt{32} \end{array} $$
The equation of tangent at $\left(x _1, y _1\right)$ is
$$ \frac{x x _1}{9}-\frac{y y _1}{4}=1 $$
From Eqs. (i) and (ii),
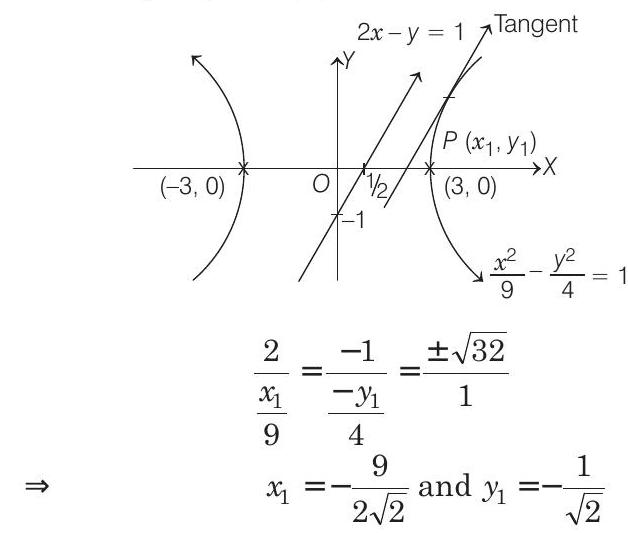
or
$$ x _1=\frac{9}{2 \sqrt{2}}, y _1=\frac{1}{\sqrt{2}} $$
