Hyperbola 2 Question 11
11. Consider the hyperbola $H: x^{2}-y^{2}=1$ and a circle $S$ with centre $N\left(x _2, 0\right)$. Suppose that $H$ and $S$ touch each other at a point $P\left(x _1, y _1\right)$ with $x _1>1$ and $y _1>0$. The common tangent to $H$ and $S$ at $P$ intersects the $X$-axis at point $M$. If $(l, m)$ is the centroid of $\triangle P M N$, then the correct expression(s) is/are
(2015 Adv.)
(a) $\frac{d l}{d x _1}=1-\frac{1}{3 x _1^{2}}$ for $x _1>1$
(b) $\frac{d m}{d x _1}=\frac{x _1}{3\left(\sqrt{x _1^{2}-1}\right)}$ for $x _1>1$
(c) $\frac{d l}{d x _1}=1+\frac{1}{3 x _1^{2}}$ for $x _1>1$
(d) $\frac{d m}{d y _1}=\frac{1}{3}$ for $y _1>0$
Show Answer
Answer:
Correct Answer: 11. (a)
Solution:
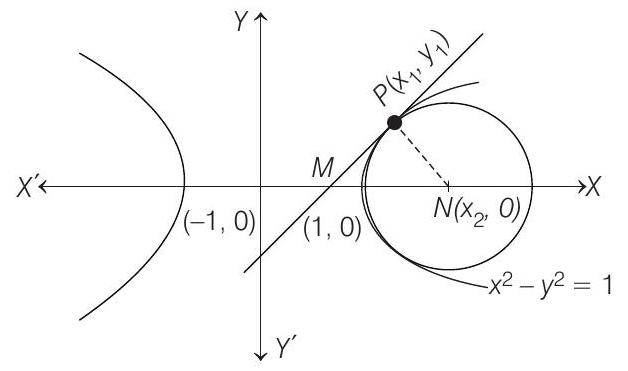
Equation of family of circles touching hyperbola at $\left(x _1, y _1\right)$ is $\left(x-x _1\right)^{2}+\left(y-y _1\right)^{2}+\lambda\left(x x _1-y y _1-1\right)=0$
Now, its centre is $\left(x _2, 0\right)$.
$$ \begin{array}{ll} \therefore & \frac{-\left(\lambda x _1-2 x _1\right)}{2}, \frac{-\left(-2 y _1-\lambda y _1\right)}{2}=\left(x _2, 0\right) \\ \Rightarrow & 2 y _1+\lambda y _1=0 \Rightarrow \lambda=-2 \\ \text { and } & 2 x _1-\lambda x _1=2 x _2 \Rightarrow x _2=2 x _1 \end{array} $$
$\therefore \quad P\left(x _1, \sqrt{x _1^{2}-1}\right)$ and $\quad N\left(x _2, 0\right)=\left(2 x _1, 0\right)$
As tangent intersect $X$-axis at $M \frac{1}{x _1}, 0$.
Centroid of $\triangle P M N=(l, m)$
$\Rightarrow \quad \frac{3 x _1+\frac{1}{x _1}}{3}, \frac{y _1+0+0}{3}=(l, m)$
$$ \Rightarrow \quad l=\frac{3 x _1+\frac{1}{x _1}}{3} $$
On differentiating w.r.t. $x _1$, we get $\frac{d l}{d x _1}=\frac{3-\frac{1}{x _1^{2}}}{3}$
$\Rightarrow \quad \frac{d l}{d x _1}=1-\frac{1}{3 x _1^{2}}$, for $x _1>1$ and $m=\frac{\sqrt{x _1^{2}-1}}{3}$
On differentiating w.r.t. $x _1$, we get
Also,
$$ \frac{d m}{d x _1}=\frac{2 x _1}{2 \times 3 \sqrt{x _1^{2}-1}}=\frac{x _1}{3 \sqrt{x _1^{2}-1}} \text { for } x _1>1 $$
On differentiating w.r.t. $y _1$, we get $\frac{d m}{d y _1}=\frac{1}{3}$, for $y _1>0$
