Functions 3 Question 2
2. If
(2004, 1M)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 2. (d)
Solution:
- We have,
Now, let us draw the graph of
Note that when
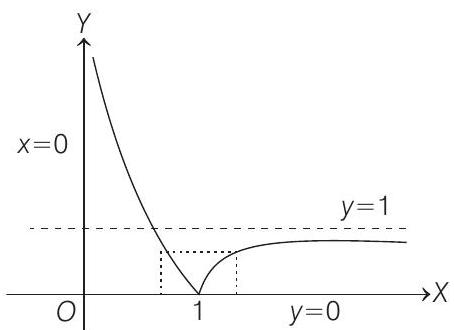
Clearly,
Also,






