Functions 1 Question 11
11. If $S$ is the set of all real $x$ such that $\frac{2 x-1}{2 x^{3}+3 x^{2}+x}$ is positive, then $S$ contains
(1986, 2M)
(a) $-\infty,-\frac{3}{2}$
(b) $-\frac{3}{2},-\frac{1}{4}$
(c) $-\frac{1}{4}, \frac{1}{2}$
(d) $\frac{1}{2}, 3$
Fill in the Blanks
Show Answer
Answer:
Correct Answer: 11. $(a, d)$
Solution:
- Since,
$$ \frac{2 x-1}{2 x^{3}+3 x^{2}+x}>0 $$
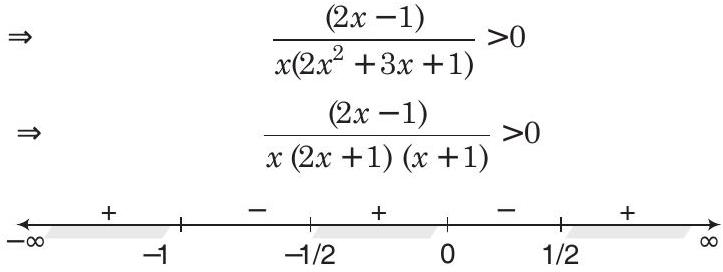
Hence, the solution set is,
$$ x \in(-\infty,-1) \cup(-1 / 2,0) \cup(1 / 2, \infty) $$
Hence, (a) and (d) are the correct options.
