Ellipse 2 Question 6
6. If tangents are drawn to the ellipse $x^{2}+2 y^{2}=2$ at all points on the ellipse other than its four vertices, then the mid-points of the tangents intercepted between the coordinate axes lie on the curve
(2019 Main, 11 Jan I)
(a) $\frac{x^{2}}{4}+\frac{y^{2}}{2}=1$
(b) $\frac{1}{4 x^{2}}+\frac{1}{2 y^{2}}=1$
(c) $\frac{x^{2}}{2}+\frac{y^{2}}{4}=1$
(d) $\frac{1}{2 x^{2}}+\frac{1}{4 y^{2}}=1$
Show Answer
Solution:
- Given equation of ellipse is $x^{2}+2 y^{2}=2$, which can be written as $\frac{x^{2}}{2}+\frac{y^{2}}{1}=1$
Let $P$ be a point on the ellipse, other than its four vertices. Then, the parametric coordinates of $P$ be $(\sqrt{2} \cos \theta, \sin \theta)$
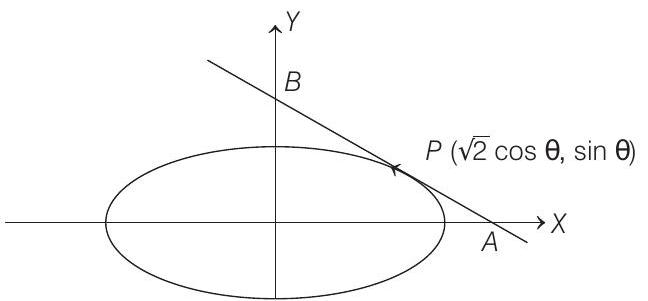
Now, the equation of tangent at $P$ is $\frac{x \sqrt{2} \cos \theta}{2}+\frac{y \sin \theta}{1}=1$
$\left[\because\right.$ equation of tangent at $\left(x _1, y _1\right)$ is given by $T=0$
$$ \Rightarrow \frac{x x _1}{a^{2}}+\frac{y y _1}{b^{2}}=1 $$
$$ \Rightarrow \quad \frac{x}{\sqrt{2} \sec \theta}+\frac{y}{\operatorname{cosec} \theta}=1 $$
$\therefore A(\sqrt{2} \sec \theta, 0)$ and $B(0, \operatorname{cosec} \theta)$
Let mid-point of $A B$ be $R(h, k)$, then
$$ \begin{aligned} h & =\frac{\sqrt{2} \sec \theta}{2} \text { and } k=\frac{\operatorname{cosec} \theta}{2} \\ 2 h & =\sqrt{2} \sec \theta \text { and } 2 k=\operatorname{cosec} \theta \\ \Rightarrow \quad \cos \theta & =\frac{1}{\sqrt{2} h} \text { and } \sin \theta=\frac{1}{2 k} \end{aligned} $$
We know that, $\cos ^{2} \theta+\sin ^{2} \theta=1$
$\therefore \quad \frac{1}{2 h^{2}}+\frac{1}{4 k^{2}}=1$
So, locus of $(h, k)$ is $\frac{1}{2 x^{2}}+\frac{1}{4 y^{2}}=1$
