SATHEE: Ellipse 2 Question 22

Ellipse 2 Question 22

22. Let $d$ be the perpendicular distance from the centre of the ellipse $x^{2} / a^{2} + y^{2} / b^{2} = 1$ to the tangent drawn at a point $P$ on the ellipse. If $F_{1}$ and $F_{2}$ are the two foci of the ellipse, then show that

${(P F_{1} - P F_{2})}^{2} = 4 a^{2} 1 - \frac{b^{2}}{d^{2}}$

$(1995, 5 M)$

Integer Type Question

Show Answer

Answer:

Correct Answer: 22. (b)

Solution:

Let the coordinates of point $P$ be $(a \cos θ, b \sin θ)$ .

Then, equation of tangent at $P$ is

$\frac{x}{a} \cos θ + \frac{y}{b} \sin θ = 1$

We have, $d =$ length of perpendicular from $O$ to the

$\begin{aligned} d & = \frac{| 0 + 0 - 1 |}{\sqrt{\frac{\cos^{2} θ}{a^{2}} + \frac{\sin^{2} θ}{b^{2}}}} \\ \Rightarrow \frac{1}{d} & = \sqrt{\frac{\cos^{2} θ}{a^{2}} + \frac{\sin^{2} θ}{b^{2}}} \\ \Rightarrow \frac{1}{d^{2}} & = \frac{\cos^{2} θ}{a^{2}} + \frac{\sin^{2} θ}{b^{2}} \end{aligned}$

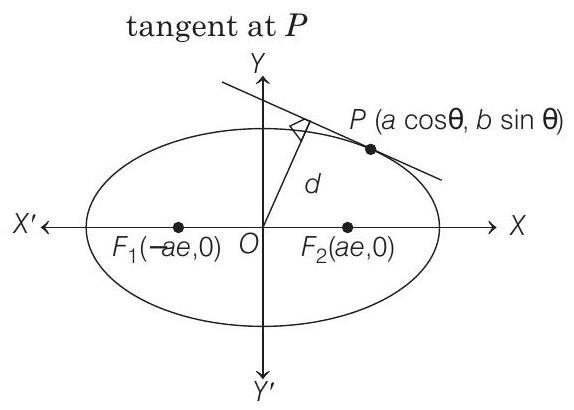
We have to prove ${(P F_{1} - P F_{2})}^{2} = 4 a^{2} 1 - \frac{b^{2}}{d^{2}}$

Now, RHS $= 4 a^{2} 1 - \frac{b^{2}}{d^{2}} = 4 a^{2} - \frac{4 a^{2} b^{2}}{d^{2}}$

$\begin{aligned} = 4 a^{2} - 4 a^{2} b^{2} \frac{\cos^{2} θ}{a^{2}} + \frac{\sin^{2} θ}{b^{2}} \\ = 4 a^{2} - 4 b^{2} \cos^{2} θ - 4 a^{2} \sin^{2} θ \\ = 4 a^{2} (1 - \sin^{2} θ) - 4 b^{2} \cos^{2} θ \\ = 4 a^{2} \cos^{2} θ - 4 b^{2} \cos^{2} θ \\ = 4 \cos^{2} θ (a^{2} - b^{2}) = 4 \cos^{2} θ \cdot a^{2} e^{2} ∵ e = \sqrt{1 - (b / a)^{2}} \end{aligned}$

Again, $P F_{1} = e | a \cos θ + a / e | = a | e \cos θ + 1 |$

$= a (e \cos θ + 1)$

$[∵ - 1 \leq \cos θ \leq 1$ and $0 < e < 1]$

Similarly, $P F_{2} = a (1 - e \cos θ)$

Therefore, $L H S = {(P F_{1} - P F_{2})}^{2}$

$\begin{aligned} = [a (e \cos θ + 1) - a (1 - e \cos θ)]^{2} \\ = (a e \cos θ + a - a + a e \cos θ)^{2} \\ = (2 a e \cos θ)^{2} = 4 a^{2} e^{2} \cos^{2} θ \end{aligned}$