Ellipse 2 Question 20
20. Let $A B C$ be an equilateral triangle inscribed in the circle $x^{2}+y^{2}=a^{2}$. Suppose perpendiculars from $A, B, C$ to the major axis of the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1,(a>b)$ meets the ellipse respectively at $P, Q, R$ so that $P, Q, R$ lie on the same side of the major axis as $A, B, C$ respectively. Prove that, the normals to the ellipse drawn at the points $P, Q$ and $R$ are concurrent.
$(2000,7$ M)
Show Answer
Answer:
Correct Answer: 20. (d)
Solution:
- Let the coordinates of $A \equiv(a \cos \theta, b \sin \theta)$, so that the coordinates of
$$ B={a \cos (\theta+2 \pi / 3), a \sin (\theta+2 \pi / 3)} $$
and $C={a \cos (\theta+4 \pi / 3), a \sin (\theta+4 \pi / 3)}$
According to the given condition, coordinates of $P$ are $(a \cos \theta b \sin \theta)$ and that of $Q$ are ${a \cos (\theta+2 \pi / 3)$, $b \sin (\theta+2 \pi / 3)}$ and that of $R$ are $a \cos (\theta+4 \pi / 3), b \sin (\theta+4 \pi / 3)$
$[\because$ it is given that $P, Q, R$ are on the same side of $X$-axis as $A, B$ and $C]$
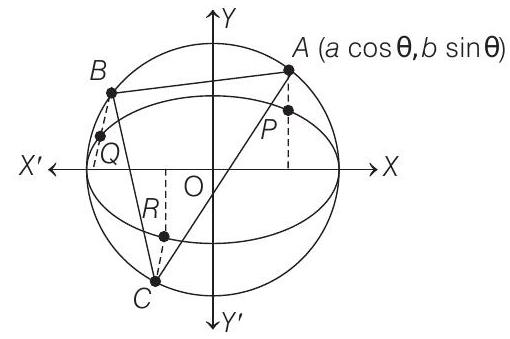
Equation of the normal to the ellipse at $P$ is
$$ \frac{a x}{\cos \theta}-\frac{b y}{\sin \theta}=a^{2}-b^{2} $$
or $a x \sin \theta-b y \cos \theta=\frac{1}{2}\left(a^{2}-b^{2}\right) \sin 2 \theta$
Equation of normal to the ellipse at $Q$ is
$a x \sin \theta+\frac{2 \pi}{3}-b y \cos \theta+\frac{2 \pi}{3}$
$$ =\frac{1}{2}\left(a^{2}-b^{2}\right) \sin 2 \theta+\frac{4 \pi}{3} $$
Equation of normal to the ellipse at $R$ is
$$ a x \sin (\theta+4 \pi / 3)-b y \cos (\theta+4 \pi / 3) $$
$$ =\frac{1}{2}\left(a^{2}-b^{2}\right) \sin (2 \theta+8 \pi / 3) $$
But $\sin (\theta+4 \pi / 3)=\sin (2 \pi+\theta-2 \pi / 3)$
$$ =\sin (\theta-2 \pi / 3) $$
and $\cos (\theta+4 \pi / 3)=\cos (2 \pi+\theta-2 \pi / 3)$
$$ =\cos (\theta-2 \pi / 3) $$
and $\sin (2 \theta+8 \pi / 3)=\sin (4 \pi+2 \theta-4 \pi / 3)$
$$ =\sin (2 \theta-4 \pi / 3) $$
Now, Eq. (iii) can be written as $a x \sin (\theta-2 \pi / 3)-b y \cos (\theta-2 \pi / 3)$
$$ =\frac{1}{2}\left(a^{2}-b^{2}\right) \sin (2 \theta-4 \pi / 3) $$
448 Ellipse
For the lines (i), (ii) and (iv) to be concurrent, we must have the determinant
$$ \Delta _1=\left|\begin{array}{rc} a \sin \theta & -b \cos \theta \\ a \sin \theta+\frac{2 \pi}{3} & -b \cos \theta+\frac{2 \pi}{3} \\ a \sin \theta-\frac{2 \pi}{3} & -b \cos \theta-\frac{2 \pi}{3} \\ \frac{1}{2}\left(a^{2}-b^{2}\right) \sin 2 \theta \\ \frac{1}{2}\left(a^{2}-b^{2}\right) \sin (2 \theta+4 \pi / 3) \\ \frac{1}{2}\left(a^{2}-b^{2}\right) \sin (2 \theta-4 \pi / 3) \end{array}\right|=0 $$
Thus, lines (i), (ii) and (iv) are concurrent.
