SATHEE: Ellipse 2 Question 17

Ellipse 2 Question 17

17. Let $E_{1}$ and $E_{2}$ be two ellipses whose centres are at the origin. The major axes of $E_{1}$ and $E_{2}$ lie along the $X$ -axis and $Y$ -axis, respectively. Let $S$ be the circle $x^{2} + (y - 1)^{2} = 2$ . The straight line $x + y = 3$ touches the curves $S, E_{1}$ and $E_{2}$ at $P, Q$ and $R$ , respectively.

Suppose that $P Q = P R = \frac{2 \sqrt{2}}{3}$ . If $e_{1}$ and $e_{2}$ are the eccentricities of $E_{1}$ and $E_{2}$ respectively, then the correct expression(s) is/are

(2015 Adv.)

(a) $e_{1}^{2} + e_{2}^{2} = \frac{43}{40}$

(b) $e_{1} e_{2} = \frac{\sqrt{7}}{2 \sqrt{10}}$

(d) $e_{1} e_{2} = \frac{\sqrt{3}}{4}$

Analytical & Descriptive Questions

Show Answer

Answer:

Correct Answer: 17. (b)

Solution:

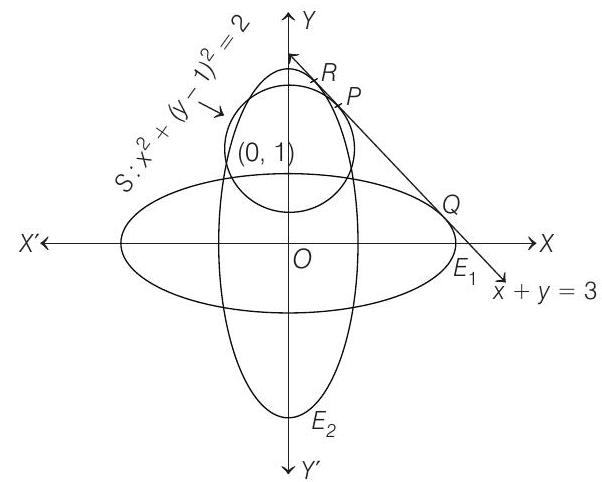
Here, $E_{1} : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1, (a > b)$ $E_{2} : \frac{x^{2}}{c^{2}} + \frac{y^{2}}{d^{2}} = 1, (c < d)$ and $S : x^{2} + (y - 1)^{2} = 2$ as tangent to $E_{1}, E_{2}$ and $S$ is $x + y = 3$ .

Let the point of contact of tangent be $(x_{1}, y_{1})$ to $S$ .

$∴ x \cdot x_{1} + y \cdot y_{1} - (y + y_{1}) + 1 = 2$

or $x x_{1} + y y_{1} - y = (1 + y_{1})$ , same as $x + y = 3$ .

$\begin{array}{ll} \Rightarrow & \frac{x_{1}}{1} = \frac{y_{1} - 1}{1} = \frac{1 + y_{1}}{3} \\ i.e. & x_{1} = 1 and y_{1} = 2 \\ ∴ & P = (1, 2) \end{array}$

Since, $P R = P Q = \frac{2 \sqrt{2}}{3}$ . Thus, by parametric form,

$\begin{aligned} \frac{x - 1}{- 1 / \sqrt{2}} & = \frac{y - 2}{1 / \sqrt{2}} = \pm \frac{2 \sqrt{2}}{3} \\ \Rightarrow & x = \frac{5}{3}, y & = \frac{4}{3} and x = \frac{1}{3}, y = \frac{8}{3} \\ ∴ & Q & = \frac{5}{3}, \frac{4}{3} and R = \frac{1}{3}, \frac{8}{3} \end{aligned}$

Now, equation of tangent at $Q$ on ellipse $E_{1}$ is

$\frac{x \cdot 5}{a^{2} \cdot 3} + \frac{y \cdot 4}{b^{2} \cdot 3} = 1$

On comparing with $x + y = 3$ , we get

$\begin{aligned} a^{2} & = 5 and b^{2} = 4 \\ e_{1}^{2} & = 1 - \frac{b^{2}}{a^{2}} = 1 - \frac{4}{5} = \frac{1}{5} \end{aligned}$

Also, equation of tangent at $R$ on ellipse $E_{2}$ is

$\frac{x \cdot 1}{a^{2} \cdot 3} + \frac{y \cdot 8}{b^{2} \cdot 3} = 1$

On comparing with $x + y = 3$ , we get

$\begin{aligned} a^{2} = 1, b^{2} = 8 \\ ∴ e_{2}^{2} = 1 - \frac{a^{2}}{b^{2}} = 1 - \frac{1}{8} = \frac{7}{8} \\ Now, e_{1}^{2} \cdot e_{2}^{2} = \frac{7}{40} \Rightarrow e_{1} e_{2} = \frac{\sqrt{7}}{2 \sqrt{10}} \\ and e_{1}^{2} + e_{2}^{2} = \frac{1}{5} + \frac{7}{8} = \frac{43}{40} \\ Also, | e_{1}^{2} - e_{2}^{2} | = | \frac{1}{5} - \frac{7}{8} | = \frac{27}{40} \end{aligned}$