Ellipse 2 Question 11
11. The normal at a point $P$ on the ellipse $x^{2}+4 y^{2}=16$ meets the $X$-axis at $Q$. If $M$ is the mid-point of the line segment $P Q$, then the locus of $M$ intersects the latusrectum of the given ellipse at the points (2009)
(a) $\pm \frac{3 \sqrt{5}}{2}, \pm \frac{2}{7}$
(b) $\pm \frac{3 \sqrt{5}}{2}, \pm \frac{\sqrt{19}}{4}$
(c) $\pm 2 \sqrt{3}, \pm \frac{1}{7}$
(d) $\pm 2 \sqrt{3}, \pm \frac{4 \sqrt{3}}{7}$
Show Answer
Solution:
- Given, $\frac{x^{2}}{16}+\frac{y^{2}}{4}=1$
[replacing $k$ by $y$ and $h$ by $x$ ]
Here,
$$ a=4, b=2 $$
Equation of normal
$$ \begin{array}{rlrl} 4 x \sec \theta-2 y \operatorname{cosec} \theta & =12 \\ & \quad M \frac{7 \cos \theta}{2}, \sin \theta & =(h, k) \\ \therefore \quad & \quad h & =\frac{7 \cos \theta}{2} \\ \Rightarrow \quad & =\frac{2 h}{7}=\cos \theta \end{array} $$
and $\quad k=\sin \theta$
On squaring and adding Eqs. (i) and (ii), we get
$$ \begin{aligned} \frac{4 h^{2}}{49}+k^{2} & =1 \quad\left[\because \cos ^{2} \theta+\sin ^{2} \theta=1\right] \\ \text { Hence, locus is } \frac{4 x^{2}}{49}+y^{2} & =1 \end{aligned} $$
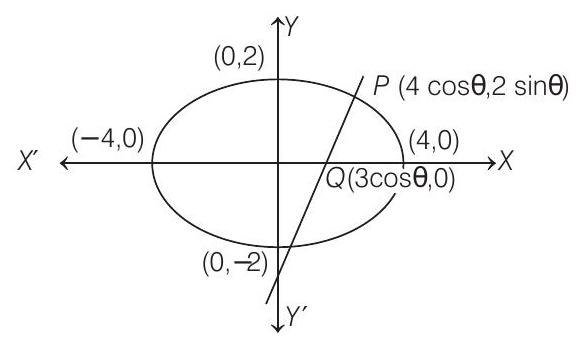
For given ellipse, $e^{2}=1-\frac{4}{16}=\frac{3}{4}$
$$ \begin{aligned} & \therefore \quad e=\frac{\sqrt{3}}{2} \\ & \therefore \quad x= \pm 4 \times \frac{\sqrt{3}}{2}= \pm 2 \sqrt{3}[\because x= \pm a e] \end{aligned} $$
On solving Eqs. (iii) and (iv), we get
$$ \begin{aligned} \frac{4}{49} \times 12+y^{2} & =1 \Rightarrow y^{2}=1-\frac{48}{49}=\frac{1}{49} \\ y & = \pm \frac{1}{7} \end{aligned} $$
$\therefore$ Required points $\pm 2 \sqrt{3}, \pm \frac{1}{7}$.
