Ellipse 1 Question 5
6. The ellipse $E _1: \frac{x^{2}}{9}+\frac{y^{2}}{4}=1$ is inscribed in a rectangle $R$ whose sides are parallel to the coordinate axes. Another ellipse $E _2$ passing through the point $(0,4)$ circumscribes the rectangle $R$. The eccentricity of the ellipse $E _2$ is
(2012)
(a) $\frac{\sqrt{2}}{2}$
(b) $\frac{\sqrt{3}}{2}$
(c) $\frac{1}{2}$
(d) $\frac{3}{4}$
Show Answer
Answer:
Correct Answer: 6. (a)
Solution:
- PLAN Equation of an ellipse is $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$
Eccentricity
$$ e^{2}=1-\frac{b^{2}}{a^{2}} $$
440 Ellipse
Description Situation As ellipse circumscribes the rectangle, then it must pass through all four vertices.
Let the equation of an ellipse $E _2$ be
$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$, where $a<b$ and $b=4$.
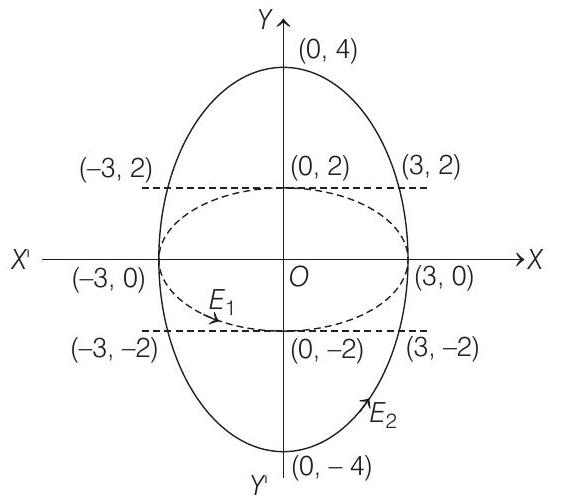
Also, it passes through $(3,2)$.
$$ \begin{array}{lll} \Rightarrow & \frac{9}{a^{2}}+\frac{4}{b^{2}}=1 & {[\because b=4]} \\ \Rightarrow & \frac{9}{a^{2}}+\frac{1}{4}=1 \quad \text { or } \quad a^{2}=12 \end{array} $$
Eccentricity of $E _2, \quad e^{2}=1-\frac{a^{2}}{b^{2}}=1-\frac{12}{16}=\frac{1}{4} \quad[\because a<b]$
$$ \therefore \quad e=\frac{1}{2} $$
