Ellipse 1 Question 4
5. The equation of the circle passing through the foci of the ellipse
(2013 Main)
(a)
(c)
(b)
(d)
Show Answer
Answer:
Correct Answer: 5. (c)
Solution:
- Given equation of ellipse is
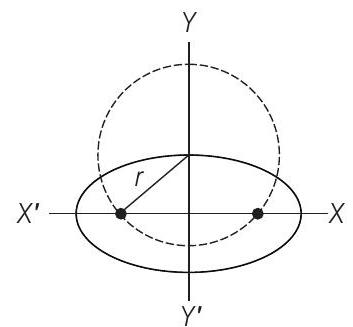
Here,
Radius of the circle,
Now, equation of circle is






